
Reti Neurali
Vai alla prima parte articolo ...
Riconoscimento Ottico dei Caratteri - Il programma VB (2° parte)
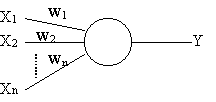
Il neurone artificiale (Fig 1) è un’unità di elaborazione che possiede una serie di ingressi una soglia ed una funzione di attivazione che determina l’uscita del neurone stesso. Gli ingressi dei neuroni possono provenire dall’esterno oppure da altri neuroni. Quando due neuroni sono interconnessi tra loro, il punto di giunzione tra i due viene detto sinapsi (in accordo con la nomenclatura adottata per il neurone biologico).
| Fig .1 - Esempio di Rete Neurale | Fig .2 -Esempio di Rete Neurale |
 |
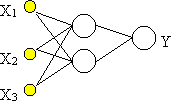 |
La Fig2 mostra un tipo di rete neurale detta FeedFarward.
Di seguito analizzeremo brevemente il tipo di neurone utilizzato nella nostra rete. Si tratta del Percettrone semplice ideato da Rosenblatt nel 1962 proprio allo scopo di riconoscere i caratteri.
Percettrone semplice
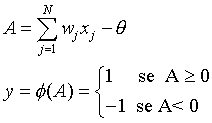 |
Eq 1.1 Eq 1.2 |
A è l’attivazione ed Xj gli ingressi. Wj sono i pesi sinaptici e q è detta soglia. Questi ultimi variano durante il processo di addestramento della rete neurale.
L’attivazione A di un neurone è data dalla combinazione lineare degli ingressi Xi con pesi Wj (Eq 1.1) . Ciò è un principio generale e vale per tutti i neuroni che sono stati ideati perché ha fondamenta biologiche.
Gli ingressi X1 , X1, X1, ….. Xn sono detti anche ingressi bipolari, perché possono assumere solo 2 valori: 1 e –1. Consideriamo il vettore X = (X1 , X1, X1, ….. Xn) . Tale vettore è detto pattern di ingresso.
La funzione f(A) può essere scelta in diversi modi. Nel nostro caso utilizzeremo la funzione non lineare sopra indicata (Eq 1.2) . Scegliendo una funzione di questo tipo si ha che:
- Se A ³ 0 Û å wi * xi ³ q allora avremo una risposta y = 1 (cioè eccitatoria)
- Se A < 0 Û å wi * xi < q allora avremo una risposta y = -1 (cioè inibitoria).
L’apprendimento consiste nel mostrare al percettrone il pattern di ingresso e la risposta che deve essere associata. I pesi sinaptici Wi e la soglia q vengono modificati in base al confronto tra la risposta effettiva del percettrone (valutata con 1.1) e la risposta desiderata.
Sia u la risposta desiderata ed y quella effettiva :
I pesi sinaptici non vengono corretti se la risposta y=u mentre vengono corretti se la risposta è diversa. Il fattore di correzione è dovuto a un psicologo canadese, Donald Hebb.
Donald Hebb scopri che nei circuiti biologici le connessioni vengono rinforzate quando due neuroni ,connessi tra loro, sono attivi contemporaneamente e viceversa. Quindi, consideriamo il fattore di correzione Dwi = xi * u e facciamo una bella tabbelluccca dove, a sinistra mettiamo u ed xi , ed a destra, metttimo Dwi. Si ha che:
u xi Dwi
1
-1 -1
-1 1 -1
-1 -1 1
1 1 1
Ohhhh ma guarda guarda. Quando l’ingresso è concorde all’uscita il contributo Dwi è negativo mentre è il viceversa quando sono discordi. Bene, sommiamo le variazioni relative ad ogni passo di addestramento come indicato nell’ Eq 1.3 sotto riportata. Sapete che cosa accade? Che, durante l’addestramento, quando xi ed u hanno lo stesso valore, wi cresce (ossia la connessione si rafforza) e quando xi ed u sono diversi, wi decresce (ossia la connessione si indebolisce).
wi(t+1) = wi(t) + Dwi(t) Eq 1.3
t indica un determinato istante
e quindi t+1 quello successivo!
In genere il fattore Dwi = xi * u viene moltiplicato
per una costante h detta tasso di apprendimento
Con tale fattore moltiplicativo si può variare la rapidità dell’addestramento (ma su questo non entreremo nel merito).
La nostra rete neurale
La prima cosa da fare prima di metterci a programmare è capire chi e l’ingresso e chi è l’uscita della rete e di quanti percettroni abbiamo bisogno.
I nostri caratteri vengono disegnati su una matrice di 6 righe per 5. Associamo ad ogni elemento della matrice un valore bipolore. Tale valore, sarà –1 se il punto della matrice è bianco, mentre varrà +1 nel caso in cui il punto è nero. In questo modo otterremo una matrice numerica che indicheremo con M. Consideriamo ad esempio la lettera “C” La matrice dei punti (a sinistra) e quella numerica (a destra) sono riportate di seguito.
| Fig 3 - Matrice numerica associata alla griglia | Fig. 4 - Griglia di rappresentazione del carattere |
Problema: l’ingresso dei neuroni è costituito da vettori mentre noi abbiamo matrici. Cosa faccimo? Semplice, realizziamo un isomorfismo tra lo spazio delle matrici e quello dei vettori. E’ un parolone per dire semplicemente che stabiliamo una semplice corrispondenza biunivoca tra vettori e le matrici. Come? Le righe della matrice vengono affiancate in sequenza in modo da formare un vettore.
Nel nostro caso il vettore di ingresso relativo alla lettera C sarà dato da:
x = (1 1 1 1 1 -1 -1 -1 -1 1 -1 -1 -1 -1 1 -1 -1 -1 -1 1 -1 -1 -1 -1 1 1 1 1)
Ok, questo per quel che riguarda gli ingressi e per le uscite ?
Bene , Utilizzeremo un percettrone per ogni carattere da apprendere.
Consideriamo un certo carattere ed il suo vettore x associato. Il percettrone che deve riconoscere questo carattere verrà addestrato in modo da fornire una risposta y=1, se al suo ingresso c’è x (o un pattern simile) mentre fornirà una risposta y = -1 negli altri casi. Nel nostro esempio il precettrone addestrato a riconoscere la C, dovrà attivarsi solo in corrispondenza al vettore x sopra indicato ed essere disattivo in tutti gli altri casi.
Oss: I precettarono hanno una caratteristica interessante. Dopo un addestramento compiuto su pattern simili (ossia caratteri simili ) il percettrone impara ad estrarre le caratteristiche di quel pattern e si attiva quando le riconosce. Questo significa che un percettrone è in grado di riconoscere un carattere mai visto prima, ma simile a quelli con qui e stato addestrato.
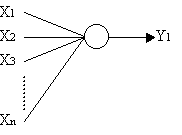
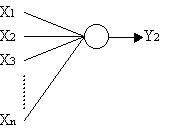
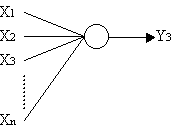
Una rete addestrata a riconoscere tre lettere sarà così fatta:
 |
 |
 |
Dove n è pari alla lunghezza di x ossia 5x6 = 30 elementi
Y1 sarà pari
a 1 solo in corrispondenza della lettera 1 (o una sua simile)
Y2 sarà
pari a 1 solo in corrispondenza della lettera 2 (o una sua simile)
Y3 sarà
pari a 1 solo in corrispondenza della lettera 3 (o una sua simile)
Mettendo insieme i tre percettroni avremo:
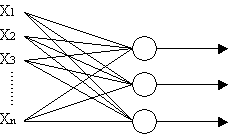 |
Y1 Y2 Y3 |
Il Programma Visual basic
Illustrerò solo le procedure principali del programma (altrimenti questo articolo non lo finisco più).
Se siete interessati a qualche chiarimento, beh… la mia mail la avete!
Vi premetto subito che il programma è commentato poco (perché mi volevo sbrigare a finirlo) inoltre, il codice non è proprio come si usa dire in informatica “Codice Pulitò”. Diciamo che è un pò alla casereccia , però funziona!
Memorizzazione
dei caratteri
Un carattere viene disegnato utilizzando un array di shape (di nome CH) organizzati sul form in modo da formare una griglia (come mostrato in figura 1). Gli elementi sono numerati in sequenza da 0 a 29. L’elemento numero CH(0) è quello in alto a sinistra sulla griglia. Spostandoci da sinistra verso destra, sulla prima riga, la numerazione cresce. L’ultimo elemento della prima riga sarà quindi CH(4). Poi si ricomincia con il primo elemento della seconda riga, che sarà CH(5), fino ad arrivare all’ultimo della seconda riga, che sarà il CH(9). Così via fino all’ultimo in basso a destra CH(29)
Come già spiegato in precedenza, i caratteri vengono memorizzati in vettori riga di 30 elementi.
Quindi,se vogliamo memorizzare 20 caratteri, avremo bisogno di una matrice di 20 righe da 30 elementi ciascuna. Indichimo con M(20,30) questa matrice.
La funzione InMat(n) memorizza un generico carattere presente sulla griglia nella riga n della matrice M.
Public Sub InMatM(n As Byte)
For i = 0 To 29
If
CH(i).BackColor = vbBlack Then
M(n, i) = 1
Else
M(n,
i) = -1
End
If
Next i
End
Sub
InMat(n) in pratica esegue una scansione da CH(0) a
CH(29). Si il generico CH(i) ha sfondo nero il corrispondente elemento
in posizione i sulla riga n viene settato ad uno e viceversa se lo sfondo
e bianco viene settato a -1
La funzione outMatM(n) fa l’operazione opposta. Data una riga di M, disegna il carattere associato sulla griglia.Il carattere associato alla riga n di M viene memorizzato nella posizione n del controllo list1. (cioè il ListBox etichettato con “ N° Cicli ” )
Il numero di neuroni è pari (come spiegato in precedenza) al numero di caratteri diversi che si vogliono far apprendere alla rete. Questi sono memorizzati in list2 (cioè il listBox etichettato con “Neuroni associati” ).
Apprendimento
Public
Sub addestra()
LBch.Caption
= ""
èta
= 1 ' imposta il tasso di apprendimento
If List2.ListCount = 0 Then
MsgBox "E' effettuare inserire almeno un
carattere!"
Exit Sub
End If
InizializzaW ‘ inizializza
la matrice dei pesi sinaptici
‘ effettua l’addestramento per ogni
neurone relativo ad un uno specifico carattere
For i = 0 To List2.ListCount - 1
Apprendi
(i)
Next
i
‘----------------------------------------------------------------------------------------
Label7.Caption
= "Addestramento Neuroni completato"
Frame1.Enabled = True
End Sub
W(20,31) è la matrice dei pesi sinaptici. La vedremo meglio di seguito.
La procedura addestra effettua l’addestramento di tutti i neuroni, uno per ogni carattere presente in list2. L’addestramento del neurone i-esimo avviene a mezzo della procedura appendi .
Analizziamola in dettaglio.
Public
Sub Apprendi(n As Integer) 'n è il neurone da addestrare
Dim X(31) As Integer, Ncicli As Byte, y
As Integer, t As Integer, dw As Integer
Dim chn As String, chx As String
chn = List2.List(n): Ncicli = List1.ListCount
- 1
For ix = 0 To Ncicli
'definisco lo stato di uscita
chx = List1.List(ix)
If chx = chn Then
t = 1
Else
t
= -1
End If
'----------------------------
'definisco il vettore delle attivazioni in ingresso
' X(0)=-1 X(1..30) vettore associato al carattere
X(0) = -1
For i = 0 To 29
X(i
+ 1) = M(ix, i)
Next i
'-----------------------------
'valuto la attivazione
somma = 0
For i = 0 To 30
somma
= somma + W(n, i) * X(i)
Next i
If somma > 0 Then
y = 1
Else
y
= -1
End If
'-------------------------------
'modifico i pesi finchè y<>t
While y <> t
For
i = 0 To 30
dw = èta * t * X(i)
W(n, i) = W(n, i) + dw
Next
i
'rivaluto
la attivazione
somma = 0
For i = 0 To 30
somma = somma + W(n, i)*X(i)
Next i
If
somma > 0 Then
y = 1
Else
y
= -1
End If
Wend
'--------------------------------
Next ix
End Sub
L’istruzione :
chn = List2.List(n)
Prende il carattere di list2 in posizione n (cioè quello relativo al neurone da addestrare).
Il ciclo for ripete tutte le istruzioni per ogni elemento di list1 (cioè tutti per tutti i pattern di addestramento forniti alla rete). Vediamo le operazioni effettuate all’interno del ciclo.
'definisco lo stato di uscita
Viene valutata l’uscita del generico neurone n, relativo al carattere chn. In particolare, il neurone dovrà emettere uscita t=1 solo nel caso in cui il carattere che si presenta in list2 è proprio chn mentre, dovrà essere –1 negli altri casi.
'definisco il vettore delle attivazioni in ingresso
Al generico carattere chx=list2.list(ix) è associato un vettore di attivazioni in ingresso. Tale vettore e memorizzato nella riga ix di M. Questa sezione del codice non fa altro che copiare tale riga nel vettore X.
Il Valore X(0) è costante vale –1. Vedremo di seguito che tale posizione serve ad includere la soglia q all’interno della sommatoria dell’eq 1.1
'valuto la attivazione
Per il calcolo dell’attivazione A è necessario valutare la sommatoria dell’eq 1.1 . Per far ciò si esegue un ciclo che accumula i prodotti W(i)X(i) nella variabile somma. Da notare che il ciclo for parte da 0! Ciò significa che viene addizionato anche il fattore iniziale w(0)*X(0). Tale fattore è la soglia, infatti, se nell’Eq1.1 poniamo:
-q =-W(0) = X(0)W(0), con X(0)=-1 possiamo inglobare la soglia all’interno della sommatoria.
L’uscita y viene valutata secondo l’eq 1.2; se: somma > 0 allora y=1 e viceversa, y=-1 quando la somma £ 0.
'modifica dei pesi
Se l’uscita y del neurone n considerato è diversa dal valore t desiderato (ciclo while con controllo in testa) , allora vengono modificati i pesi secondo il fattore di Hebb. Successivamente viene rivalutata l’attivazione e l’uscita y. Se y è uguale all’uscita desiderata t, si passa ad addestrare lo stesso neurone con il puttern successivo di list1 altrimenti , si ripete il ciclo while.
Riconoscimento
Il riconoscimento è molto semplice. Viene costruito il vettore di ingresso X.
X(0)=-1 (Il motivo l’ ho spiegato prima!)
X(i) =1 se lo shape è nero e viceversa X(i)=-1 se lo sciape è bianco.
Consideriamo che, ad ogni carattere corrisponde un neurone; ossia ad ogni carattere da riconoscere corrisponde una riga di W (che definisce i pesi sinaptici per il neurone in esame).
Il ciclo For j per ogni carattere di list2 valutata l’attivazione.
Il Neurone per il quale la somma >0 sarà quello relativo alla lettera disegnata nella griglia.
Se list2 viene scansionato tutto e nessun neurone genera somma>0 significa che il carattere non è stato riconosciuto . La procedura restituisce List2.ListIndex = -1 per indicare questo fatto.
OSS La procedura riconosci si arresta non appena trova un neurone
che ha somma>0. Questo però non garantisce che non ci sia un altro
neurone successivo con somma>0 . In altre parole il programma non rileva
se ci sono eventuali interferenze. Lascio a voi il compito!
Public
Sub Riconosci()
Dim X(31) As Integer
'definisco il vettore delle attivazioni in ingresso
' X(0)=-1 X(1..30) vettore associato al carattere
X(0) = -1
For i = 1 To 30
If
CH(i - 1).BackColor = vbBlack Then
X(i)
= 1
Else
X(i)
= -1
End
If
Next i
'-----------------------------
List2.ListIndex = -1
For j = 0 To List2.ListCount - 1
List2.ListIndex
= List2.ListIndex + 1
'valuto la attivazione
per il neurone j
somma = 0
For i = 0 To 30
somma
= somma + W(j, i) * X(i)
Next i
If somma > 0 Then Exit Sub
Next j
List2.ListIndex = -1
End Sub